How To Make A Mandelbrot Set

This article will walk you through how to draw the MandelBrot gear up in Google Sheets, using simply formulas and the built-in chart tool.

What Is The MandelBrot Set?

The Mandelbrot set is a grouping of special numbers with some astonishing properties.

You've almost certainly seen an image of the Mandelbrot set before.

It'south one of the most famous mathematical concepts, known exterior of mathematical circles even. It's named later on the French mathematician, Benoit Mandelbrot, who was the father of fractal geometry.

The Mandelbrot gear up is fantastically beautiful. It's an exquisite work of art, generated by a unproblematic equation.

More than formally, the Mandelbrot set is the set of complex numbers c, for which the equation z² + c does not diverge when iterated from z = 0.

Gosh, what does that hateful?

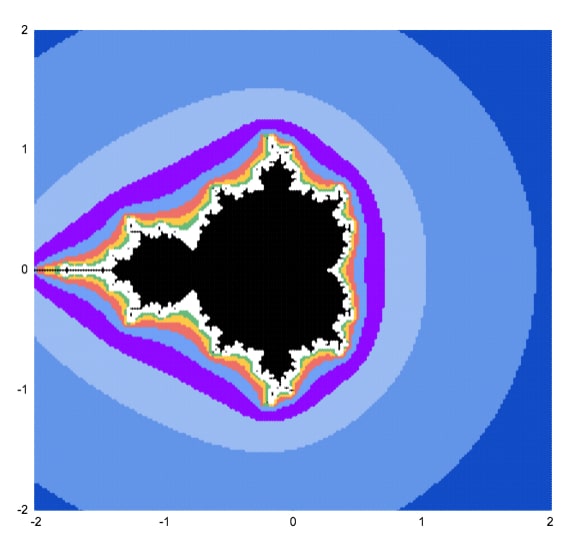
Well, it's easier if you expect at the picture at the meridian of this article. The black area represents points that do non run abroad to infinity when you keep applying the equation z² + c.

Consider c = -ane.

It repeats -1, 0, -1, 0, -1… forever, so it never escapes. It'southward bounded so it belongs in the Mandelbrot ready.

Now consider c = one.

Starting with z = 0, the first iteration is 1.

The second iteration is 1² + ane = 2.

The tertiary iteration is two² + 1 = v.

The fourth iteration is v² + i = 26.

And so on 26, 677, 458330, 210066388901, … Information technology blows upward!

It diverges to infinity, then it is not in the Mandelbrot fix.

Earlier we can draw the Mandelbrot set, we need to think almost circuitous numbers.

Imaginary And Complex Numbers

Information technology'southward impossible to draw the Mandelbrot set without a bones agreement of complex numbers.

If you lot're new to complex numbers, have a read of this primer article first: Complex Numbers in Google Sheets

It explains what complex numbers are and how you use them in Google Sheets.

To recap, complex numbers are numbers in the form

a + bi

where i is the square root of -1.

We tin can plot them every bit coordinates on a 2-dimensional plane, where the real coefficient "a" is the x-centrality and the imaginary coefficient "b" is on the y-axis.

Use A Scatter Plot To Draw The Mandelbrot Set

Taking each point on this ii-d plane in turn, we test it to see if it belongs to the Mandelbrot set. If it does vest, it gets ane color. If it doesn't belong, information technology gets a different color.

This scatter plot chart of colored points is an approximate view of the Mandelbrot set.

Equally we increment the number of points plotted and the number of iterations nosotros go successively more than detailed views of the Mandelbrot set. A point that may still exist < 2 on iteration three may be clearly exterior that purlieus past iteration five, vii or ten.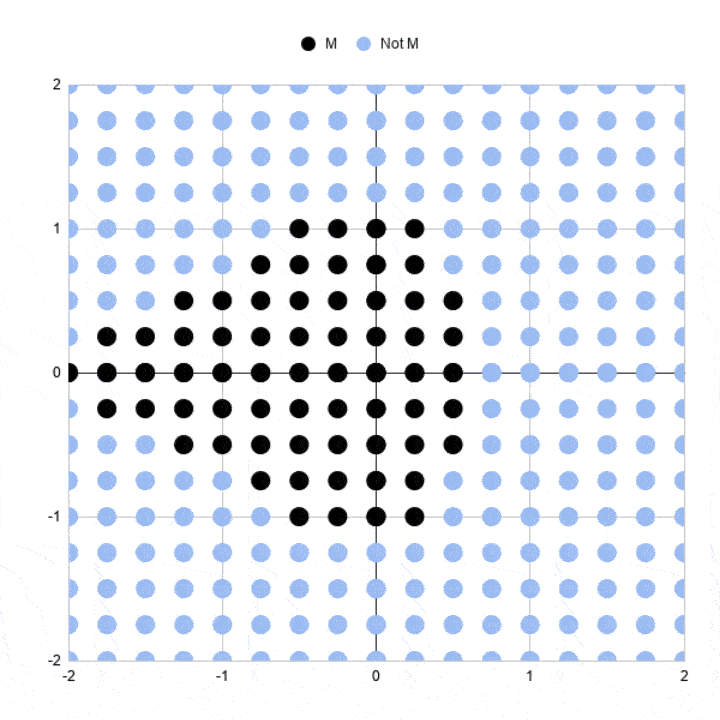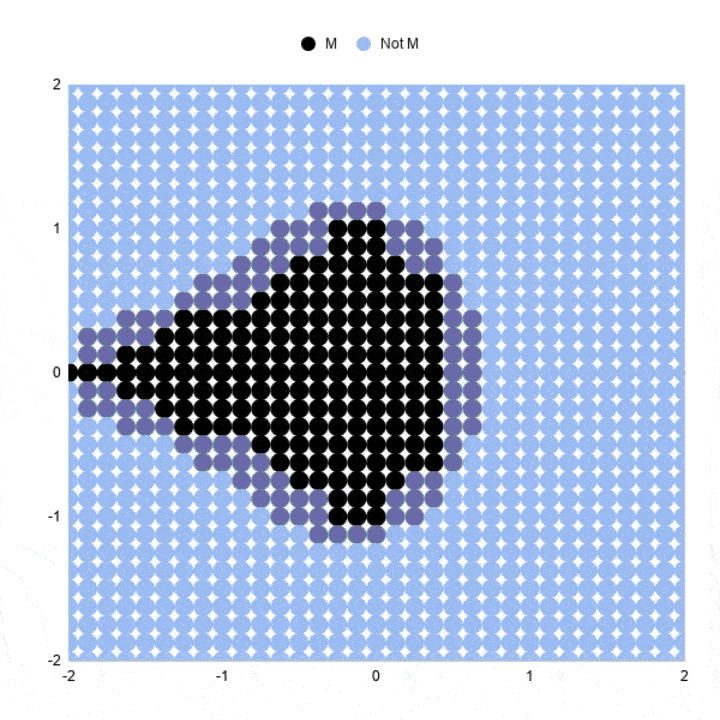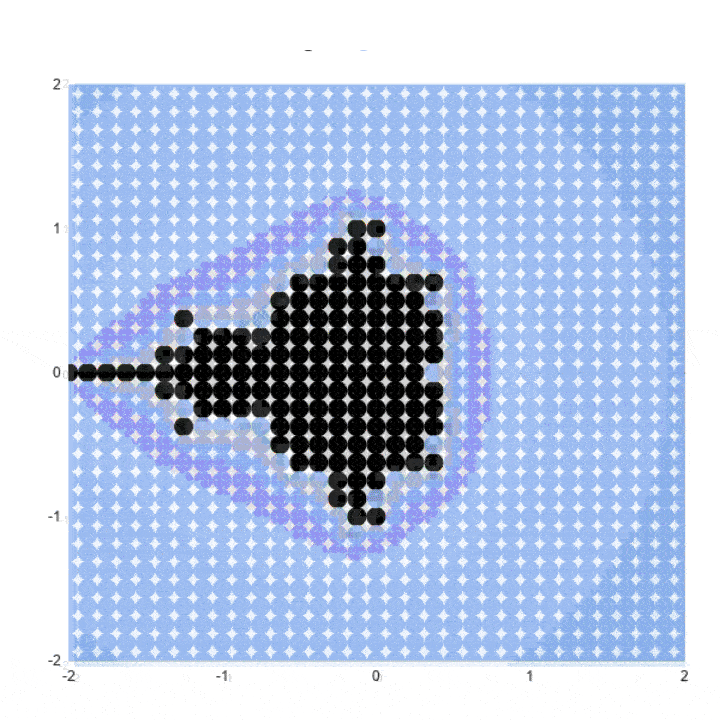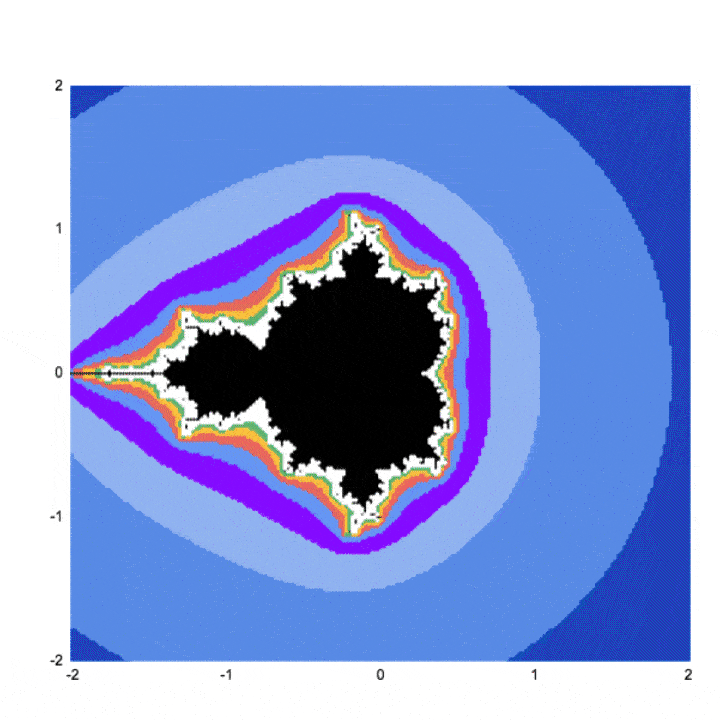

You lot can see the outline resembles the Mandelbrot ready much more clearly at college iterations.

How To Describe The MandelBrot Gear up In Google Sheets, Using Only Formulas

Hither'south a simple approximation of the Mandelbrot set drawn in Google Sheets:

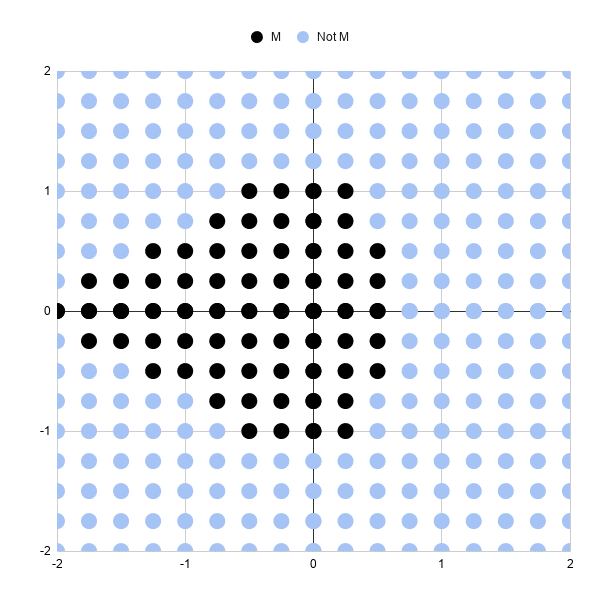
Let's run through the steps to create information technology.

It's a scatter plot with 289 points (17 past 17 points).

Each point is colored to show whether it's in the Mandlebrot set or non, subsequently 3 iterations.

Black points stand for circuitous numbers, which are only coordinates (a,b) remember, whose sizes are notwithstanding less than or equal to 2 subsequently 3 iterations. So we're including them in our Mandelbrot set up.

Light blue points correspond complex numbers whose sizes have grown larger than 2 and are non in our Mandelbrot set. In other words, they're diverging.

Three iterations are not very many, which is why this nautical chart is a very crude approximation of the Mandelbrot set. Some of these black points volition eventually diverge on higher iterations.

And plainly, we need more than points so we can fill in the gaps between the points and test those circuitous numbers.

But it'south a first.

Generating The Complex Number Coordinates

In column A, we need the sequence going from 0 to 2 and repeating { 0, 0.25, 0.five, 0.75, i, 1.25, i.5, ane.75, two, 0, 0.25, 0.v, …}

In column B, we need the sequence 0, and then 0.25, so 0.5 repeating ix times each until we reach 2 { 0, 0, 0, 0, 0, 0, 0, 0, 0, 0.25, 0.25, 0.25, …}

This gives us the combinations of x and y coordinates for our complex numbers c that we'll test to see if they lie in the ready or non.

It'due south easier to see in the actual Sheet:

We go on going until we reach number ii in column B. We have 324 rows of information. There are some repeated rows (similar 0,0) but that doesn't matter for at present.

Columns A and B at present incorporate the coordinates for our grid of complex numbers. Now we need to test each 1 to see if it belongs in the Mandelbrot set up.

Formulas For The Mandelbrot Algorithm

We create the algorithm steps in columns C through J.

In cell C2, we create the circuitous number by combining the real and imaginary coefficients:

=Circuitous(A2,B2)

Cell D2 contains the first iteration of the algorithm with z = 0, so the result is equal to C, the complex number in cell C2, hence:

=C2

The second iteration is in jail cell E2. The equation this time is z² + c, where z is the value in cell D2 and C is the value from C2:

=IMSUM(IMPOWER(D2,ii),$C2)

It's the same z² + c in F2, where z in this example is from E2 (the previous iteration):

=IMSUM(IMPOWER(E2,2),$C2)

Notice the "$" sign in front of the C in both formulas in columns E and F. This is to lock our formula dorsum to the C value for our Mandelbrot equation.

In cell G2:

=IMABS(D2)

Drag this formula across cells H2 and I2 likewise.

In cell J2, use the IFERROR function:

=IFERROR(IF(I2<=2,1,ii),2)

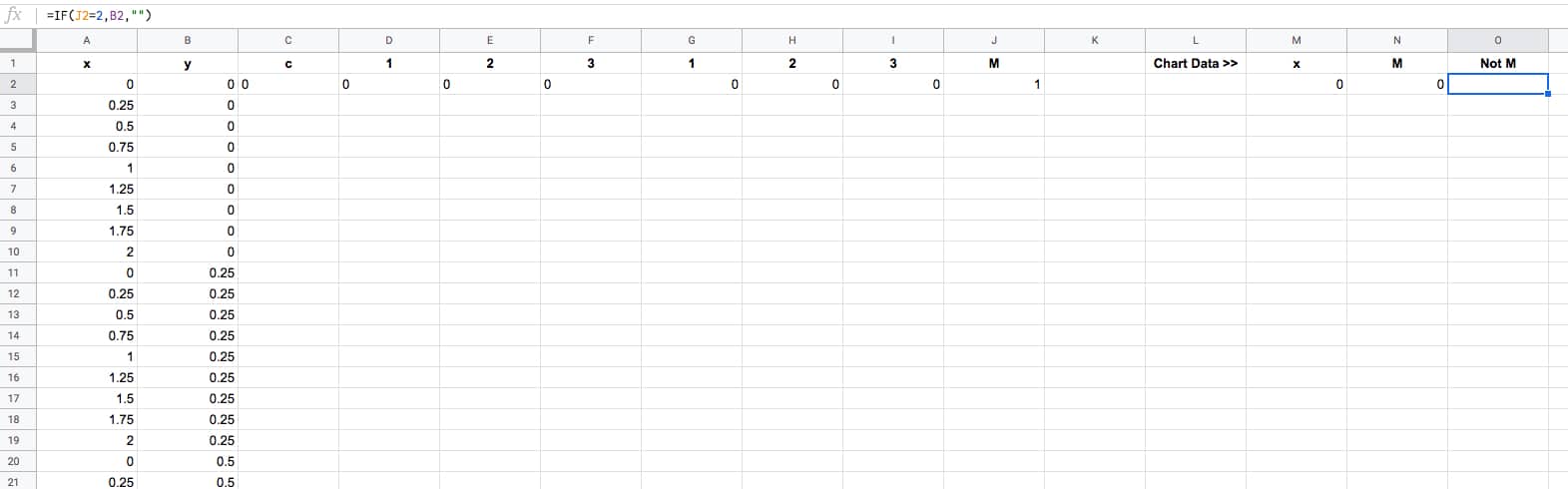
And so leave a couple of blank columns, before putting the chart data in columns M, Northward and O, with the post-obit formulas representing the x values and the ii y series with different colors:

=A2

=IF(J2=one,B2,"")

=IF(J2=2,B2,"")

Thus, our dataset now looks like this (click to enlarge):

The final job is to drag that commencement row of formulas down to the bottom of the dataset, so that every row is filled in with the formulas (click to overstate):

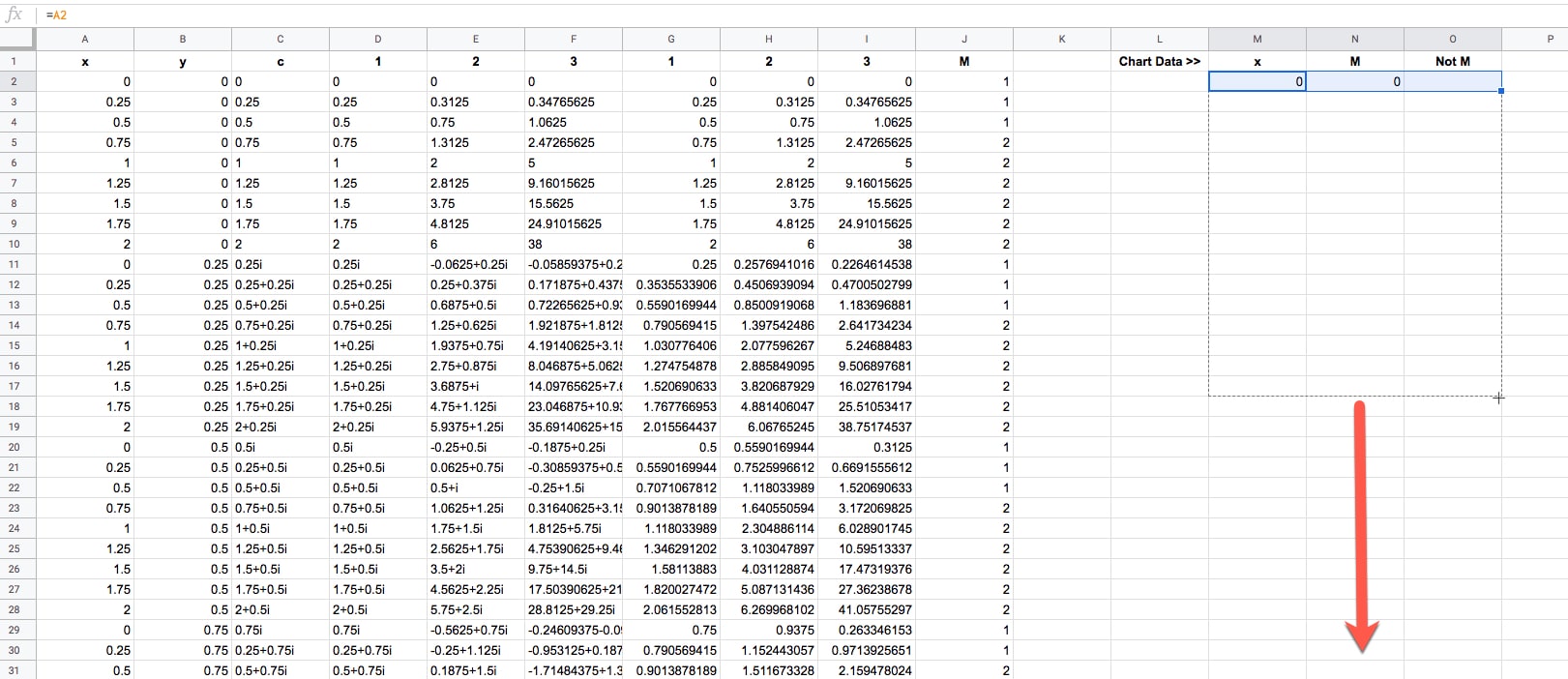
Ok, now nosotros're ready to draw some pretty pictures!

Drawing The Mandelbrot Set In Google Sheets

Highlight columns M, North and O in your dataset.

Click Insert > Chart.

It'll open to a weird looking default Cavalcade Chart, so change that to a Scatter chart under Setup > Nautical chart type.

Change the series colors if you want to make the Mandelbrot set up black and the non-Mandelbrot set some other color. I chose light bluish.

And finally, resize your chart into a square shape, using the black grab handles on the borders of the chart object.

Blast! There information technology is in all information technology's glory:

Note: you may need to manually ready the min and max values of the horizontal and vertical axes to be -2 and 2 respectively in the Customize menu of the nautical chart editor.

How To Draw A Better MandelBrot Set in Google Sheets

Generating Data Automatically

Generating those ten-y coordinates manually is extremely tedious and non actually practical beyond the simple instance above.

Thankfully you lot can use the awesome SEQUENCE function, UNIQUE function, and Assortment Formulas in Google Sheets to assistance you out.

This formula will generate the x-y coordinates for a 33 by 33 grid, which gives a more filled-in image than the uncomplicated case above.

=ArrayFormula(UNIQUE({
MOD(SEQUENCE(289,ane,0,1),17)/viii,
ROUNDDOWN(SEQUENCE(289,1,0,ane)/17)/8;
-Modern(SEQUENCE(289,i,0,1),17)/8,
ROUNDDOWN(SEQUENCE(289,1,0,ane)/17)/viii;
MOD(SEQUENCE(289,1,0,i),17)/8,
-ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8;
-MOD(SEQUENCE(289,one,0,i),17)/8,
-ROUNDDOWN(SEQUENCE(289,1,0,1)/17)/8
}))

Then drag the other formulas down your rows to complete the dataset as we did to a higher place.

Then yous can highlight columns M, Due north, and O to draw your chart once again.

Notation: yous may demand to manually set the min and max values of the horizontal and vertical axes to exist -ii and 2 respectively in the Customize menu of the chart editor.

With three iterations, the chart looks like:

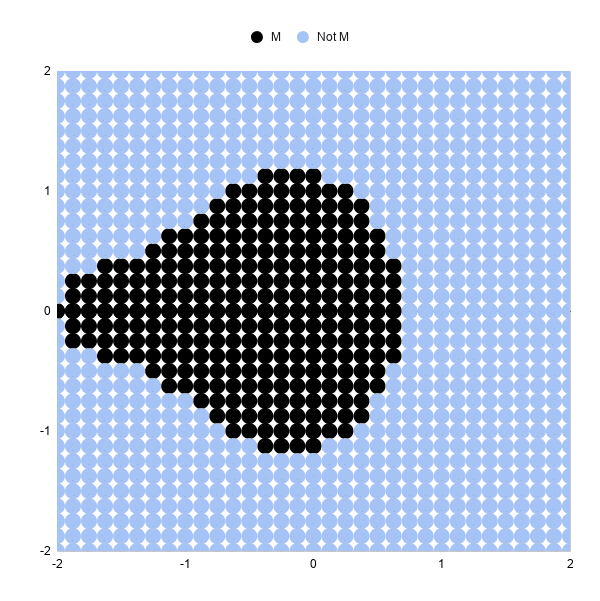
Increasing The Iterations

Permit's look at 5 iterations and ten iterations, and you'll meet how much detail this adds.

To move from 3 iterations to 5, nosotros need to add some columns to our Canvas and repeat the algorithm two more times.

And then, insert two bare columns betwixt F and G. Label the headings 4 and 5.

Elevate the formula in F2 beyond the new bare columns G and H (this is the z² + c equation as a Google Canvas formula):

In G2:

=IMSUM(IMPOWER(F2,2),$C2)

In H2:

=IMSUM(IMPOWER(G2,2),$C2)

We demand to add the respective size calculation columns. Between Grand and 50, insert two new blank columns and drag the IMABS formula across.

Now in L2:

=IMABS(G2)

And in M2:

=IMABS(H2)

Finally, update the IF formula to ensure it's testing the value in cavalcade M now:

=IFERROR(IF(M2<=2,i,ii),ii)

And that's information technology!

Our chart should update and await similar this:

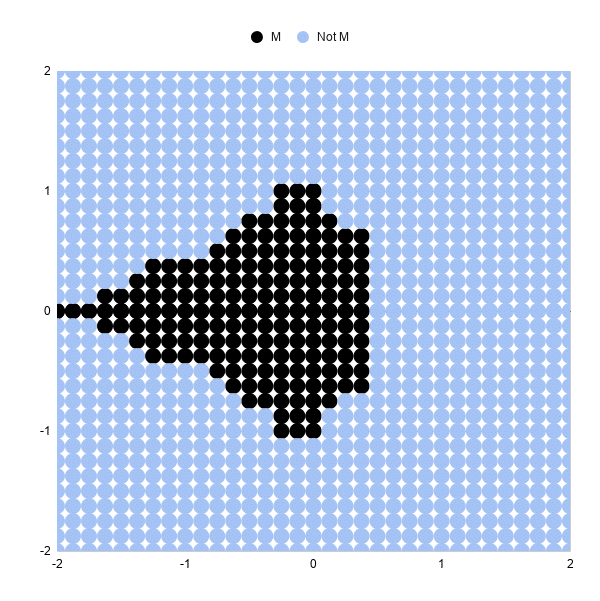
You can see the shape of the Mandelbrot fix much more clearly at present.

Increasing from 5 iterations to 10 iterations is exactly the aforementioned. Add 5 blank columns and populate with the formulas once again.

The resulting x iteration nautical chart is amend again:

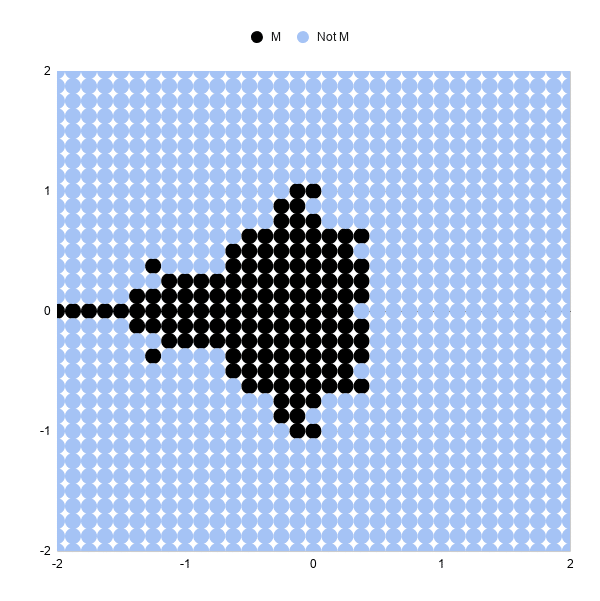
Increasing The Number Of Data Points

Increasing the number of points to 6,561 in an 81 by 81 filigree will give a more "complete" moving-picture show than the examples to a higher place.

This sequence formula will generate these datapoints:

=ArrayFormula(UNIQUE({
Modernistic(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20;
-Modernistic(SEQUENCE(1681,1,0,1),41)/20,
ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/xx;
Modernistic(SEQUENCE(1681,i,0,i),41)/twenty,
-ROUNDDOWN(SEQUENCE(1681,ane,0,1)/41)/20;
-MOD(SEQUENCE(1681,i,0,ane),41)/20,
-ROUNDDOWN(SEQUENCE(1681,1,0,1)/41)/20
}))

Exist warned, every bit you increase the number of formulas in your Sail and the number of points to plot in your scatter chart, your Sheet will start to slow downwards!

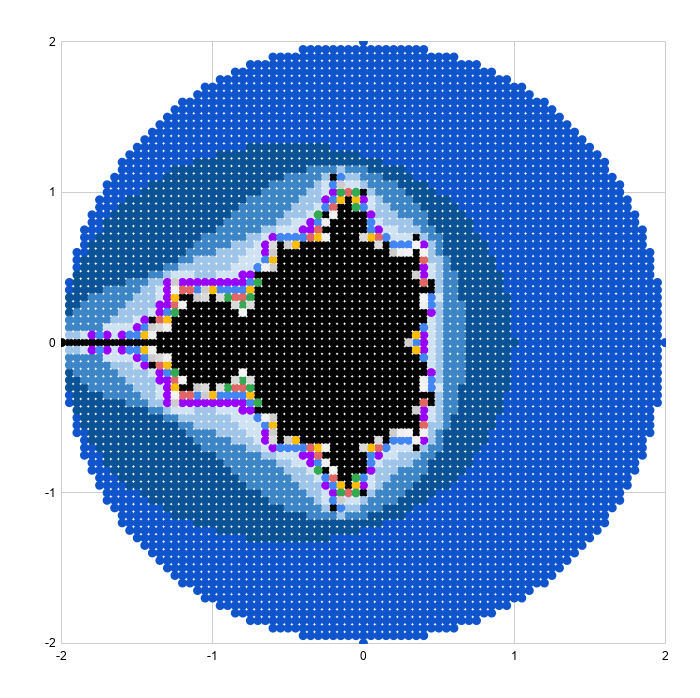
Adding Color Bands

We can add color bands to show which iteration a given indicate "escaped" towards infinity.

For example, all of the points that are larger than our threshold on iteration v get a different colour than those that are less than the threshold at iteration 5, but become larger on iteration 6.

The formulas for the iterations and size are the aforementioned as the examples higher up.

And so I determine if the bespeak is withal in the Mandelbrot set:

=IF(ISERROR(AG2),"No",IF(AG2<=2,"Aye","No"))

And then what iteration it "escapes" to infinity, or beyond the threshold of 2 in this example:

=IF(AH2="Yes",0,MATCH(two,S2:AG2,1))

These formulas are shown in the Google Sheets template:

Next, we create the series for the chart:

First, the Mandelbrot prepare:

=IF(AH2="Aye",B2,"")

Then series 1 to fifteen:

=IF($AI2=AK$ane,$B2,"")

The range for the besprinkle plot is then:

A1:A6562,AJ1:AY6562

where column A is the x-axis values and columns AJ to AY are the y-axis series.

Drawing the scatter plot and adjusting the series colors results in a pretty picture (this is an 81 past 81 grid):

Reaching Google Sheets Applied Limit

As a last practice, I increased the plot size to twoscore,401 representing a grid of 201 by 201 points. This really slowed the sail down and took about half an hr to render the scatter plot, and so not something I'd recommend.

The picture is very pretty though!

The twoscore,401 x-y coordinates can exist generated with this array formula:

=ArrayFormula(UNIQUE({
Mod(SEQUENCE(10201,1,0,1),101)/50,
ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/fifty;
-MOD(SEQUENCE(10201,1,0,i),101)/50,
ROUNDDOWN(SEQUENCE(10201,1,0,1)/101)/50;
MOD(SEQUENCE(10201,1,0,one),101)/50,
-ROUNDDOWN(SEQUENCE(10201,1,0,i)/101)/50;
-MOD(SEQUENCE(10201,ane,0,1),101)/50,
-ROUNDDOWN(SEQUENCE(10201,1,0,ane)/101)/fifty
}))

Zooming In On The Mandelbrot Set up

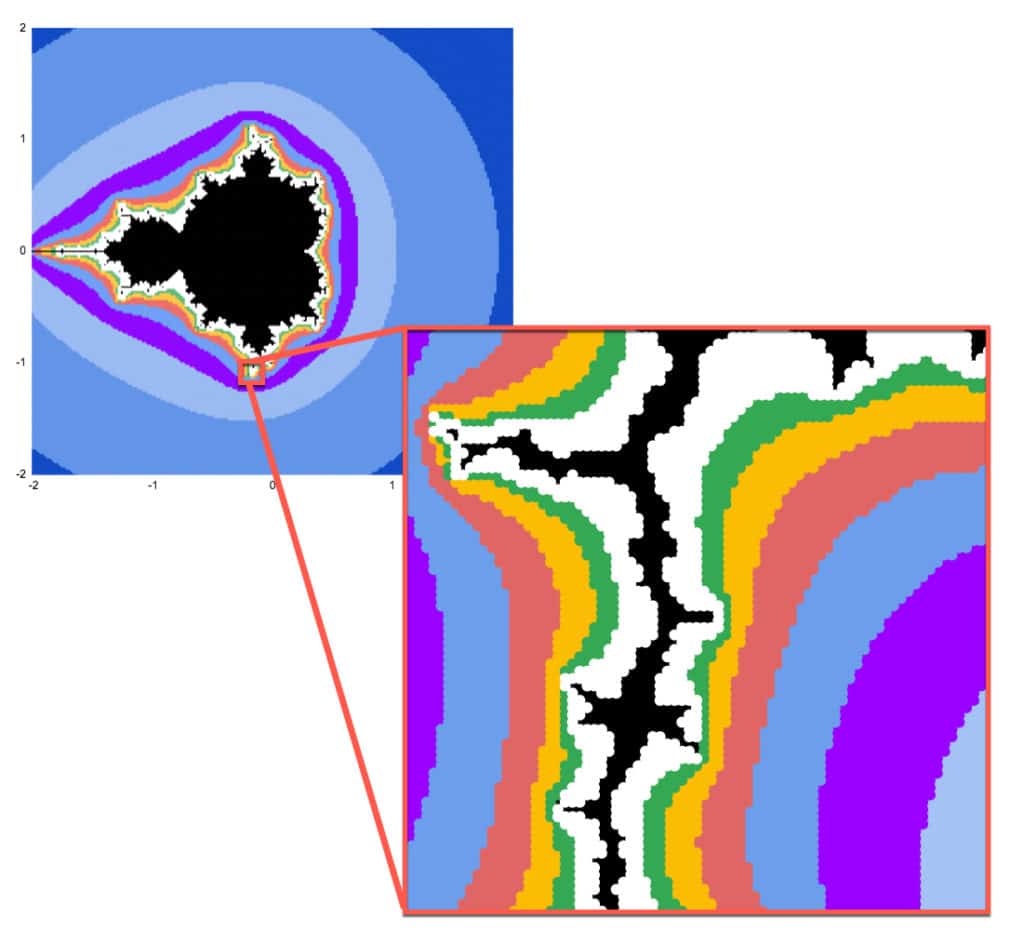
Mandelbrot sets have the belongings of cocky-similarity.

That is, nosotros can zoom in on any section of the chart and meet the aforementioned fractal geometry playing out on infinitely smaller scales. This is but one of the astonishing properties of the Mandelbrot set.

Google Sheets is definitely not the best tool for exploring the Mandelbrot set at increasing resolution. It's too irksome to render graphically and also transmission to brand the changes to the formulas and axis bounds.

However, equally the maxim says: the best tool is the i you accept to hand.

So, if you want to explore in Google Sheets it is possible:

Generating Zoomed Data

I'm going to zoom in on the betoken: -0.17033700000, -1.06506000000

(Thanks to this commodity, The Mandelbrot at a Glance by Paul Bourke, which highlighted some interesting points to explore.)

Starting with this formula in prison cell A2 to generate the vi,561 data points (I wouldn't recommend going to a higher place this considering information technology becomes as well slow):

=ArrayFormula(UNIQUE({
Modernistic(SEQUENCE(1681,1,0,one),41)/20,
ROUNDDOWN(SEQUENCE(1681,i,0,1)/41)/twenty;
-MOD(SEQUENCE(1681,1,0,one),41)/xx,
ROUNDDOWN(SEQUENCE(1681,1,0,i)/41)/20;
Modernistic(SEQUENCE(1681,1,0,1),41)/20,
-ROUNDDOWN(SEQUENCE(1681,ane,0,ane)/41)/20;
-Modern(SEQUENCE(1681,1,0,i),41)/20,
-ROUNDDOWN(SEQUENCE(1681,one,0,1)/41)/20
}))

In columns C and D, I transformed this data past change the 0,0 eye to -0.17033700000, -1.06506000000 then adding the values from A and B to C and D respectively, divided by 100 to zoom in.

=C$2+A3/100

=D$2+B3/100

The rest of the procedure is identical.

I set the nautical chart axes min and max values to friction match the min and max values in each of column C (x centrality) and D (y axis).

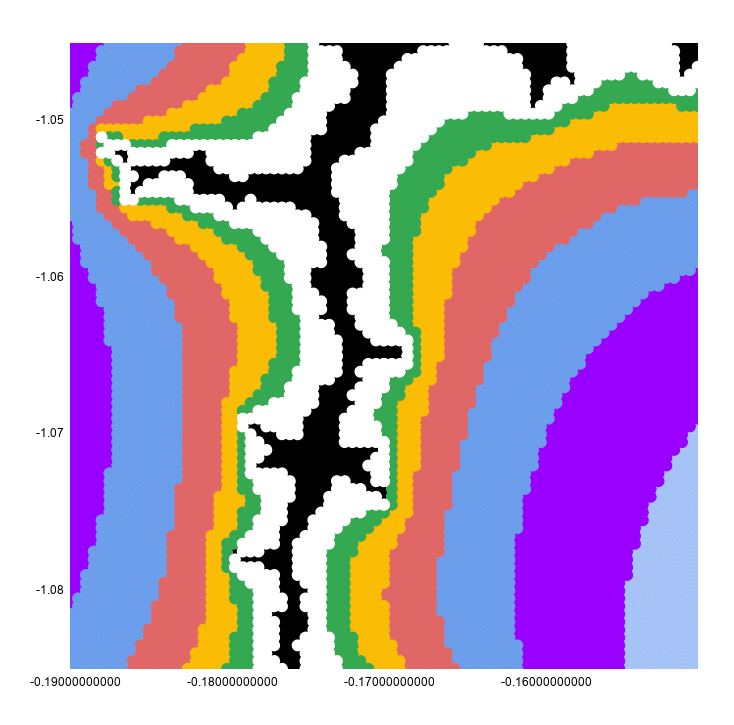
This looks continuous because the nautical chart has a betoken size of 10px to make it look better.

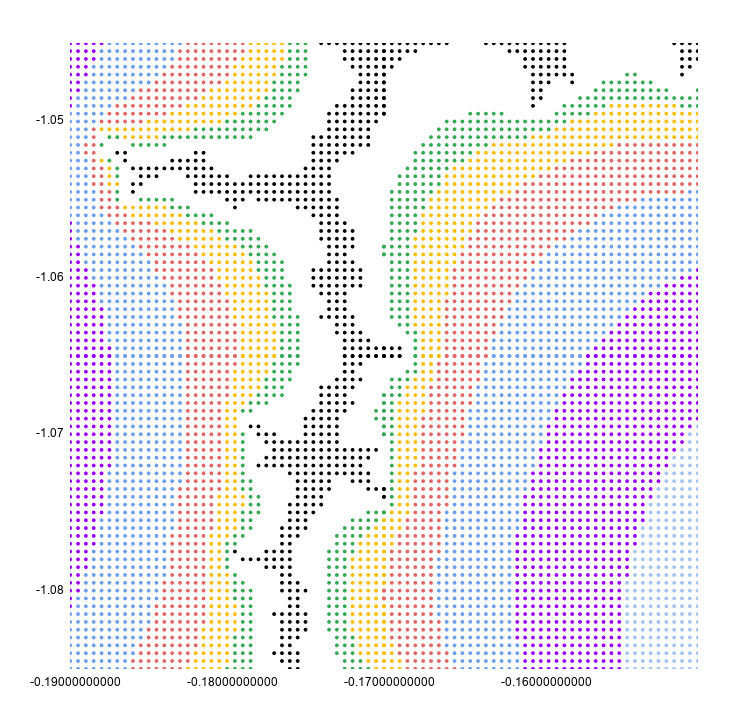
If I reset that to 2px, you can see clearly that this is still a scatter plot:

I promise you enjoyed that exploration of the Mandelbrot set in Google Sheets! Allow me know your thoughts in the comments below.

See Also

How To Draw The Cantor Gear up In Google Sheets

How To Draw The Sierpiński Triangle In Google Sheets

How To Make A Mandelbrot Set,

Source: https://www.benlcollins.com/spreadsheets/how-to-draw-the-mandelbrot-set/

Posted by: balderastheassy.blogspot.com

Share this post